|
6 | 6 |
|
7 | 7 | # 1. 分词的基本原理 |
8 | 8 |
|
9 | | - 现代分词都是基于统计的分词,而统计的样本内容来自于一些标准的语料库。假如有一个句子:“小明来到荔湾区”,我们期望语料库统计后分词的结果是:"小明/来到/荔湾/区",而不是“小明/来到/荔/湾区”。那么如何做到这一点呢? |
| 9 | +现代分词都是基于统计的分词,而统计的样本内容来自于一些标准的语料库。假如有一个句子:“小明来到荔湾区”,我们期望语料库统计后分词的结果是:"小明/来到/荔湾/区",而不是“小明/来到/荔/湾区”。那么如何做到这一点呢? |
10 | 10 |
|
11 | | - 从统计的角度,我们期望"小明/来到/荔湾/区"这个分词后句子出现的概率要比“小明/来到/荔/湾区”大。如果用数学的语言来说说,如果有一个句子S,它有m种分词选项如下:$$A_{11}A_{12}...A_{1n_1}A_{21}A_{22}...A_{2n_2}...... ......A_{m1}A_{m2}...A_{mn_m}$$ |
| 11 | +从统计的角度,我们期望"小明/来到/荔湾/区"这个分词后句子出现的概率要比“小明/来到/荔/湾区”大。如果用数学的语言来说说,如果有一个句子S,它有m种分词选项如下:$$A_{11}A_{12}...A_{1n_1}A_{21}A_{22}...A_{2n_2}...... ......A_{m1}A_{m2}...A_{mn_m}$$ |
12 | 12 |
|
13 | | - 其中下标$$n_i$$代表第i种分词的词个数。如果我们从中选择了最优的第r种分词方法,那么这种分词方法对应的统计分布概率应该最大,即:$$r = arg\;max(i)\;\;P(A_{i1},A_{i2},...,A_{in_i})$$ |
| 13 | +其中下标$$n_i$$代表第i种分词的词个数。如果我们从中选择了最优的第r种分词方法,那么这种分词方法对应的统计分布概率应该最大,即:$$r = arg\;max(i)\;\;P(A_{i1},A_{i2},...,A_{in_i})$$ |
14 | 14 |
|
15 | | - 但是我们的概率分布$$P(A_{i1},A_{i2},...,A_{in_i})$$并不好求出来,因为它涉及到$$n_i$$个分词的联合分布。在NLP中,为了简化计算,我们通常使用马尔科夫假设,即每一个分词出现的概率仅仅和前一个分词有关,即:$$P(A_{ij}|A_{i1},A_{i2},...,A_{i(j-1)}) = P(A_{ij}|A_{i(j-1)})$$ |
| 15 | +但是我们的概率分布$$P(A_{i1},A_{i2},...,A_{in_i})$$并不好求出来,因为它涉及到$$n_i$$个分词的联合分布。在NLP中,为了简化计算,我们通常使用马尔科夫假设,即每一个分词出现的概率仅仅和前一个分词有关,即:$$P(A_{ij}|A_{i1},A_{i2},...,A_{i(j-1)}) = P(A_{ij}|A_{i(j-1)})$$ |
16 | 16 |
|
17 | | - 在前面我们讲MCMC采样时,也用到了相同的假设来简化模型复杂度。使用了马尔科夫假设,则我们的联合分布就好求了,即:$$P(A_{i1},A_{i2},...,A_{in_i}) = P(A_{i1})P(A_{i2}|A_{i1})P(A_{i3}|A_{i2})...P(A_{in_i}|A_{i(n_i-1)})$$ |
| 17 | +在前面我们讲MCMC采样时,也用到了相同的假设来简化模型复杂度。使用了马尔科夫假设,则我们的联合分布就好求了,即:$$P(A_{i1},A_{i2},...,A_{in_i}) = P(A_{i1})P(A_{i2}|A_{i1})P(A_{i3}|A_{i2})...P(A_{in_i}|A_{i(n_i-1)})$$ |
18 | 18 |
|
19 | | - 而通过我们的标准语料库,我们可以近似的计算出所有的分词之间的二元条件概率,比如任意两个词$$w_1,w_2$$,它们的条件概率分布可以近似的表示为: |
| 19 | +而通过我们的标准语料库,我们可以近似的计算出所有的分词之间的二元条件概率,比如任意两个词$$w_1,w_2$$,它们的条件概率分布可以近似的表示为: |
20 | 20 |
|
21 | 21 | $$P(w_2|w_1) = \frac{P(w_1,w_2)}{P(w_1)} \approx \frac{freq(w_1,w_2)}{freq(w_1)}$$ |
22 | 22 |
|
23 | 23 | $$P(w_1|w_2) = \frac{P(w_2,w_1)}{P(w_2)} \approx \frac{freq(w_1,w_2)}{freq(w_2)}$$ |
24 | 24 |
|
25 | | - 其中$$freq(w_1,w_2)$$表示$$w_1,w_2$$在语料库中相邻一起出现的次数,而其中$$freq(w_1),freq(w_2)$$分别表示$$w_1,w_2$$在语料库中出现的统计次数。 |
| 25 | +其中$$freq(w_1,w_2)$$表示$$w_1,w_2$$在语料库中相邻一起出现的次数,而其中$$freq(w_1),freq(w_2)$$分别表示$$w_1,w_2$$在语料库中出现的统计次数。 |
26 | 26 |
|
27 | | - 利用语料库建立的统计概率,对于一个新的句子,我们就可以通过计算各种分词方法对应的联合分布概率,找到最大概率对应的分词方法,即为最优分词。 |
| 27 | +利用语料库建立的统计概率,对于一个新的句子,我们就可以通过计算各种分词方法对应的联合分布概率,找到最大概率对应的分词方法,即为最优分词。 |
28 | 28 |
|
29 | 29 | # 2. N元模型 |
30 | 30 |
|
31 | | - 当然,你会说,只依赖于前一个词太武断了,我们能不能依赖于前两个词呢?即:$$P(A_{i1},A_{i2},...,A_{in_i}) = P(A_{i1})P(A_{i2}|A_{i1})P(A_{i3}|A_{i1},A_{i2})...P(A_{in_i}|A_{i(n_i-2)},A_{i(n_i-1)})$$ |
| 31 | +当然,你会说,只依赖于前一个词太武断了,我们能不能依赖于前两个词呢?即:$$P(A_{i1},A_{i2},...,A_{in_i}) = P(A_{i1})P(A_{i2}|A_{i1})P(A_{i3}|A_{i1},A_{i2})...P(A_{in_i}|A_{i(n_i-2)},A_{i(n_i-1)})$$ |
32 | 32 |
|
33 | | - 这样也是可以的,只不过这样联合分布的计算量就大大增加了。我们一般称只依赖于前一个词的模型为二元模型\(Bi-Gram model\),而依赖于前两个词的模型为三元模型。以此类推,我们可以建立四元模型,五元模型,...一直到通用的N元模型。越往后,概率分布的计算复杂度越高。当然算法的原理是类似的。 |
| 33 | +这样也是可以的,只不过这样联合分布的计算量就大大增加了。我们一般称只依赖于前一个词的模型为二元模型\(Bi-Gram model\),而依赖于前两个词的模型为三元模型。以此类推,我们可以建立四元模型,五元模型,...一直到通用的N元模型。越往后,概率分布的计算复杂度越高。当然算法的原理是类似的。 |
34 | 34 |
|
35 | | - 在实际应用中,N一般都较小,一般都小于4,主要原因是N元模型概率分布的空间复杂度为$$O(|V|^N)$$,其中\|V\|为语料库大小,而N为模型的元数,当N增大时,复杂度呈指数级的增长。 |
| 35 | +在实际应用中,N一般都较小,一般都小于4,主要原因是N元模型概率分布的空间复杂度为$$O(|V|^N)$$,其中\|V\|为语料库大小,而N为模型的元数,当N增大时,复杂度呈指数级的增长。 |
36 | 36 |
|
37 | 37 | N元模型的分词方法虽然很好,但是要在实际中应用也有很多问题,首先,某些生僻词,或者相邻分词联合分布在语料库中没有,概率为0。这种情况我们一般会使用拉普拉斯平滑,即给它一个较小的概率值,这个方法在[朴素贝叶斯算法原理小结](/ml/bayes/po-su-bei-xie-si.md)也有讲到。第二个问题是如果句子长,分词有很多情况,计算量也非常大,这时我们可以用下一节维特比算法来优化算法时间复杂度。 |
38 | 38 |
|
39 | 39 | # 3. 维特比算法与分词 |
40 | 40 |
|
41 | | - 为了简化原理描述,我们本节的讨论都是以二元模型为基础。 |
| 41 | +为了简化原理描述,我们本节的讨论都是以二元模型为基础。 |
42 | 42 |
|
43 | | - 对于一个有很多分词可能的长句子,我们当然可以用暴力方法去计算出所有的分词可能的概率,再找出最优分词方法。但是用维特比算法可以大大简化求出最优分词的时间。 |
| 43 | +对于一个有很多分词可能的长句子,我们当然可以用暴力方法去计算出所有的分词可能的概率,再找出最优分词方法。但是用维特比算法可以大大简化求出最优分词的时间。 |
44 | 44 |
|
45 | | - 大家一般知道维特比算法是用于隐式马尔科夫模型HMM解码算法的,但是它是一个通用的求序列最短路径的方法,不光可以用于HMM,也可以用于其他的序列最短路径算法,比如最优分词。 |
| 45 | +大家一般知道维特比算法是用于隐式马尔科夫模型HMM解码算法的,但是它是一个通用的求序列最短路径的方法,不光可以用于HMM,也可以用于其他的序列最短路径算法,比如最优分词。 |
46 | 46 |
|
47 | | - 维特比算法采用的是动态规划来解决这个最优分词问题的,动态规划要求局部路径也是最优路径的一部分,很显然我们的问题是成立的。首先我们看一个简单的分词例子:"人生如梦境"。它的可能分词可以用下面的概率图表示: |
| 47 | +维特比算法采用的是动态规划来解决这个最优分词问题的,动态规划要求局部路径也是最优路径的一部分,很显然我们的问题是成立的。首先我们看一个简单的分词例子:"人生如梦境"。它的可能分词可以用下面的概率图表示: |
48 | 48 |
|
49 | 49 | 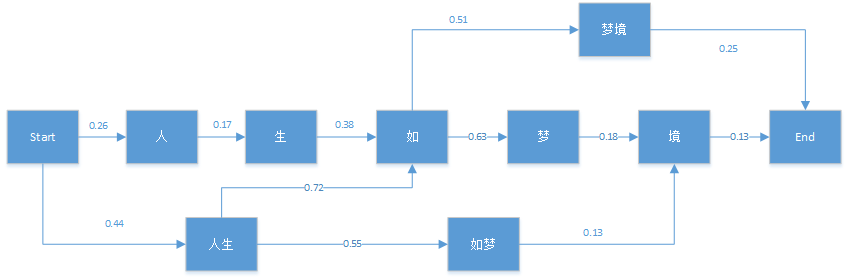 |
50 | 50 |
|
51 | | - 图中的箭头为通过统计语料库而得到的对应的各分词条件概率。比如P(生|人)=0.17。有了这个图,维特比算法需要找到从Start到End之间的一条最短路径。对于在End之前的任意一个当前局部节点,我们需要得到到达该节点的最大概率$$\delta$$,和记录到达当前节点满足最大概率的前一节点位置$$\Psi$$。 |
| 51 | +图中的箭头为通过统计语料库而得到的对应的各分词条件概率。比如P\(生\|人\)=0.17。有了这个图,维特比算法需要找到从Start到End之间的一条最短路径。对于在End之前的任意一个当前局部节点,我们需要得到到达该节点的最大概率$$\delta$$,和记录到达当前节点满足最大概率的前一节点位置$$\Psi$$。 |
52 | 52 |
|
53 | | - 我们先用这个例子来观察维特比算法的过程。首先我们初始化有:$$\delta$$(人) = 0.26$$\;\;\Psi$$(人)$$=Start$$\;\;\delta$$(人生)$$ = 0.44\;\;$$\Psi$$(人生)$$=Start$$ |
| 53 | +我们先用这个例子来观察维特比算法的过程。首先我们初始化有:$$\delta$$\(人\) = 0.26$$\;\;\Psi$$\(人\)$$=Start$$\;\;\delta$$(人生)$$ = 0.44\;\;$$\Psi$$\(人生\)$$=Start$$ |
54 | 54 |
|
55 | | - 对于节点"生",它只有一个前向节点,因此有:$$\delta$$(生) $$= \delta$$(人)$$P$$(生|人)$$ = 0.0442 \;\; \Psi$$(生)$$=$$人 |
| 55 | +对于节点"生",它只有一个前向节点,因此有:$$\delta$$\(生\) $$= \delta$$\(人\)$$P$$\(生\|人\)$$ = 0.0442 \;\; \Psi$$\(生\)$$=$$人 |
56 | 56 |
|
57 | | - 对于节点"如",就稍微复杂一点了,因为它有多个前向节点,我们要计算出到“如”概率最大的路径:$$\delta$$(如)$$ = max\{\delta$$(生)$$P$$(如|生)$$,$$\delta$$(人生)$$P$$(如|人生)$$} = max\{0.01680, 0.3168\} = 0.3168 \;\; \Psi$$(如)$$ = $$人生 |
| 57 | +对于节点"如",就稍微复杂一点了,因为它有多个前向节点,我们要计算出到“如”概率最大的路径:$$\delta$$\(如\)$$ = max\{\delta$$\(生\)$$P$$\(如\|生\)$$,$$\delta$$(人生)$$P$$(如|人生)$$} = max{0.01680, 0.3168} = 0.3168 \;\; \Psi$$(如)$$ = $$人生 |
58 | 58 |
|
59 | | - 类似的方法可以用于其他节点如下: |
| 59 | +类似的方法可以用于其他节点如下: |
60 | 60 |
|
61 | | -$$\delta$$(如梦) $$= \delta$$(人生)$$P$$(如梦|人生)$$ = 0.242 \;\; \Psi$$(如梦)$$=人生 |
| 61 | +$$\delta$$\(如梦\) $$= \delta$$\(人生\)$$P$$\(如梦\|人生\)$$ = 0.242 \;\; \Psi$$\(如梦\)$$=人生 |
62 | 62 |
|
63 | | -$$\delta$$(梦) $$= \delta$$(如)$$P$$(梦|如)$$ = 0.1996 \;\; \Psi$$(梦)$$=如 |
| 63 | +$$\delta$$\(梦\) $$= \delta$$\(如\)$$P$$\(梦\|如\)$$ = 0.1996 \;\; \Psi$$\(梦\)$$=如 |
64 | 64 |
|
65 | | -$$\delta$$(境)$$ = max\{\delta$$(梦)$$P$$(境|梦)$$ ,\delta$$(如梦)$$P$$(境|如梦)$$}= max\{0.0359, 0.0315\} = 0.0359 \;\; \Psi$$(境)=梦 |
| 65 | +$$\delta$$\(境\)$$ = max\{\delta$$\(梦\)$$P$$\(境\|梦\)$$ ,\delta$$\(如梦\)$$P$$\(境\|如梦\)}$$= max\{0.0359, 0.0315\} = 0.0359 \;\; \Psi$$\(境\)=梦 |
66 | 66 |
|
67 | | -$$\delta$$(梦境)$$ = \delta$$(梦境)$$P$$(梦境|如)$$ = 0.1585 \;\; \Psi$$(梦境)=如 |
| 67 | +$$\delta$$\(梦境\)$$ = \delta$$\(梦境\)$$P$$\(梦境\|如\)$$ = 0.1585 \;\; \Psi$$\(梦境\)=如 |
68 | 68 |
|
69 | | - 最后我们看看最终节点End: |
| 69 | +最后我们看看最终节点End: |
70 | 70 |
|
71 | | -$$\delta(End) = max\{\delta$$(梦境)$$P$$(End|梦境), $$\delta$$(境)$$P$$(End|境)$$} = max\{0.0396, 0.0047\} = 0.0396\;\;\Psi$$(End)=梦境 |
| 71 | +$$\delta(End) = max\{\delta$$\(梦境\)$$P$$\(End\|梦境\), $$\delta$$\(境\)$$P$$\(End\|境\)}$$ = max\{0.0396, 0.0047\} = 0.0396\;\;\Psi$$\(End\)=梦境 |
72 | 72 |
|
73 | | - 由于最后的最优解为“梦境”,现在我们开始用$$\Psi$$反推: |
| 73 | +由于最后的最优解为“梦境”,现在我们开始用$$\Psi$$反推: |
74 | 74 |
|
75 | | -$$\Psi(End)=$$梦境 $$\to \Psi$$(梦境)=如 $$\to \Psi$$(如)=人生 $$\to \Psi$$(人生)=start |
| 75 | +$$\Psi(End)=$$梦境 $$\to \Psi$$\(梦境\)=如 $$\to \Psi$$\(如\)=人生 $$\to \Psi$$\(人生\)=start |
76 | 76 |
|
77 | | - 从而最终的分词结果为"人生/如/梦境"。是不是很简单呢。 |
| 77 | +从而最终的分词结果为"人生/如/梦境"。是不是很简单呢。 |
78 | 78 |
|
79 | | - 由于维特比算法我会在后面讲隐式马尔科夫模型HMM解码算法时详细解释,这里就不归纳了。 |
| 79 | +由于维特比算法我会在后面讲隐式马尔科夫模型HMM解码算法时详细解释,这里就不归纳了。 |
80 | 80 |
|
81 | 81 | # 4. 常用分词工具 |
82 | 82 |
|
83 | | - 对于文本挖掘中需要的分词功能,一般我们会用现有的工具。简单的英文分词不需要任何工具,通过空格和标点符号就可以分词了,而进一步的英文分词推荐使用[nltk](http://www.nltk.org/)。对于中文分词,则推荐用[结巴分词](https://github.com/fxsjy/jieba/)(jieba)。这些工具使用都很简单。你的分词没有特别的需求直接使用这些分词工具就可以了。 |
| 83 | +对于文本挖掘中需要的分词功能,一般我们会用现有的工具。简单的英文分词不需要任何工具,通过空格和标点符号就可以分词了,而进一步的英文分词推荐使用[nltk](http://www.nltk.org/)。对于中文分词,则推荐用[结巴分词](https://github.com/fxsjy/jieba/)(jieba)。这些工具使用都很简单。你的分词没有特别的需求直接使用这些分词工具就可以了。 |
84 | 84 |
|
85 | 85 | # 5. 结语 |
86 | 86 |
|
87 | | - 分词是文本挖掘的预处理的重要的一步,分词完成后,我们可以继续做一些其他的特征工程,比如向量化(vectorize),TF-IDF以及Hash trick,这些我们后面再讲。 |
| 87 | +分词是文本挖掘的预处理的重要的一步,分词完成后,我们可以继续做一些其他的特征工程,比如向量化(vectorize),TF-IDF以及Hash trick,这些我们后面再讲。 |
88 | 88 |
|
0 commit comments